Ежи Медушевский. Георг Кантор о Дедекинде, Кронекере и о самом себе

2,118 просмотров всего, 2 просмотров сегодня

 

 

 

 

 

Ежи Медушевский. (Польша) Математик, историк математики

 

Предисловие переводчика

Великий немецкий математик Георг Кантор, создатель теории множеств, родился в Петербурге в 1845 году в семье купца Георга Вольдемара Кантора и Марии Кантор (Бём), дочери первого солиста Петербурга, скрипача Франца Бёма. Его семья была тесно связана с петербургской культурой. В 1856 году из- за болезни отца Канторы переехали в Германию. Георг Кантор учился в По­литехникуме в Цюрихе, затем в Берлинском университете, а затем всю жизнь работал в университете города Галле.

В статье известного польского математика и историка математики профес­сора Ежи Медушевского от лица Кантора воспроизводится тот трудный период его жизни, когда созданная им теория ещё не обрела признания и подвергалась нападкам коллег. Дружба Кантора с немецким математиком Рихардом Деде- киндом одарила его внимательным собеседником и деликатным критиком, но и эта дружба иногда омрачалась обидами. Другой его коллега и друг, шведский математик Геста Миттаг-Леффлёр, публиковал работы Кантора в своём жур­нале Acta mathematica, но его осторожное отношение к новаторским идеям Кантора также вызывало обиды последнего. В конце жизни к Кантору пришло мировое признание, но последние его годы были омрачены нервной болезнью.

ГЕОРГ КАНТОР О ДЕДЕКИНДЕ, КРОНЕКЕРЕ И О САМОМ СЕБЕ

Математика — это в большей степени
искусство ставить вопросы…

Г. Кантор (Диссертация)

Если бы автором был Георг Кантор, история была бы приблизительно такой же, как эта.

Множества. Я вижу множества как бесчисленные вихри песчинок, частицы которых невозможно увидеть¹. Можем ли мы что-нибудь сделать с ними? Можно ли сосчитать количество их элементов? Можем ли мы от­личить один от другого? Какой из них первый, если они бесчисленны? Но я бы хотел рассматривать множества прежде чисел. Так я хотел бы ограни­чить их изучение качественным методом. Для того, чтобы сравнить мно­жества, я бы попытался исчерпать элементы одного множества с помощью элементов другого. Чтобы сделать это, я бы попытался прикрепить один к другому. Тогда была бы нужда в некоторых геометрических методах, но их тоже надо бы исключить как зависящие от предвосхищающих основа­ний математики. Это непросто — разделить поровну бесконечное множе­ство², если оно лишено какой-либо формы. Должен ли я согласиться с Дедекиндом³, который утверждает, что множества уже даны в контексте, из которого наследуют свою форму и даже динамику? Кронекер сказал, что нет ничего кроме формулы. Я не согласен с такими ограничениями. Я счи­таю, что множества первичны по отношению к другим математическим понятиям.

Я не боюсь бесконечных множеств. Более того, я думаю, что в бес­конечности есть истинная природа множеств. Больцано, о котором я по­следнее время много слышу, допускает бесконечные множества, но он боится парадоксов, которые возникают при сведении различных аспек­тов множеств в одно рассуждение. Как и Галилей, он сомневался, можно ли признать равенство множеств, если между их элементами установлено взаимно-однозначное соответствие. Но я в силах рассмотреть такое соот­ветствие. Во всяком случае, в отличие от мнения людей, далёких от матема­тики, в изучении бесконечности не так уж много поэзии. Вопросы о бес­конечности рождаются в наших мыслях, многие из них словно нежеланные гости, хоть и с некоторым очарованием. Нашей задачей является придать им форму, индивидуальность и динамику.

Вещи, которые Кант назвал «вещи в себе», не требуют от нас такого внимания. Они имеют форму и красоту сами по себе. Камень падает по траектории, геометрия создаёт круги и спирали живых форм без чьей-то воли. Мы можем созерцать эти события, будучи свободными от необходи­мости создания математики для их понимания, природа создаёт всё это на наших глазах. Хотя в природе уже изначально заложены числа, нам присуща потребность считать. Животные, братья наши меньшие, не считают. Зем­ле не интересно знать, сколько оборотов вокруг Солнца она совершила.

Числа. Человеческое ли это творение? Они служат нам в повседневной жизни. Однако перед нами они быстро обнаруживают свою удивительную природу. Несмотря на то, что мы считаем числа творениями нашего ума, в их высшем смысле мы попадаем в положение Пигмалиона, чувствуя, что они подчиняются собственным законам, которые, наверное, нам не подвластны.

Число, не всегда желанное, вошло в геометрию и физику, чрезвычайно расширив пространство этих наук, так же как и собственные возможности.

За последние века геометрия в корне изменилась, и то же можно сказать об анализе. Мы не знаем иной цели такого расширения математики, кроме как свободного слияния с природой.

Ожидают ли и множества в будущем своего Пигмалиона? Сначала это ничто не предвещает. Множества — это tabula rasa. Дедекинд говорит, что они используются, например, в той алгебре, которая была им разработана. Вопрос в том, откуда они взялись? Они родились в мире наших мыслей. Но владеем ли мы полностью этим миром?

Моисей Мендельсон. Дедекинд говорит, что нет необходимости при­влекать пространство или время для изучения происхождения чисел. В этом он близок Моисею Мендельсону⁴, который, в отличие от Канта, с большой осторожностью относился к изучению математических аспектов филосо­фии. Мендельсон сомневался в математическом характере геометрии. Гео­метрия рассматривает вещи «in concreto», писал он. Геометрические фигу­ры уже есть, в то время как истинная математика рассматривает вещи «in abstracto», имея в виду различные примеры этой мысленной ситуации. Чис­ла не имеют очертаний. Золотые слова сказал Дедекинд в работе «Was sind und was sollen die Zahlen?» («Что такое числа и для чего они служат?»): «Числа — это вольные творения человеческого разума, они служат сред­ством более лёгкого и точного понимания различия вещей». Мендельсон поместил арифметику среди «прочих наук».

Множества прежде чисел. Дедекинд утверждает, что множества могут быть использованы как основное понятие в объяснении появления в на­шем мозгу понятия числа в смысле множеств и операций над ними. По сло­вам Кронекера, числа — божественное создание, но Дедекинд в этом идёт гораздо дальше. В качестве ключа к дальнейшим рассуждениям он исполь­зует операцию над множествами, называемую взаимно-однозначным со­ответствием, имеющую тот же уровень значимости, что и сами множества. Эта операция соответствует мысленному акту связи множества, элементы которого определены единственным образом, с другим множеством. В слу­чае взаимно-однозначного соответствия ни один элемент не соответству­ет двум или более элементам другого множества. Дедекинд рассматривает конечные множества как такие, которые не допускают взаимно-одно­значного соответствия со своими подмножествами. Понятие числа в этом определении не появляется!

Из поездки по Альпам я запомнил его дальнейшие рассуждения. Он сосредоточил внимание на множестве, названном им «мир S наших мыс­лей». Этот мир как поток. Для каждой мысли есть мысль об этой мысли, так что он заключил, что этот поток бесконечен. Выбрав минимальный подпо­ток, возникающий в нашем сознании 1, он получает индуктивную систему натуральных чисел 1, 2,…

Я не против этой красивой истории, словно взятой прямо у Шопен­гауэра. Дедекинд со своими поисками происхождения арифметики напо­минает мне такой же поиск Гельмгольца в физике и Римана в геометрии. Современная математика питается потоком идей философов, изобилую­щих золотыми суждениями. Многие из них схоластичны, например, Вейерштрасс, который утверждал, что наименьшая верхняя граница непрерыв­ной функции, определённой на замкнутом отрезке, есть значение функции. Схоластическая фраза, устоявшая перед современным анализом.

Числовая лестница. Когда я в детских грёзах считал 1, 2,… до бесконеч­ности, я повторял, что до небес можно считать и дальше, чем 1, 2,… Хотя лестница до небес бесконечна, лишь пересечение барьеров представляет проблему, дальнейшее путешествие по небу так же просто, как и по земле. Эти детские рассуждения о бесконечном подобны тем, что можно услышать от богословов. Тем не менее я испытывал те же чувства при математическом рассуждении о тригонометрических рядах, удаляя постепенно из линейных множеств их части, состоящие из изолированных точек. Бывают множества, которые и после бесконечного числа шагов остаются неисчерпанными, ещё остаётся много точек, и процедура может повторяться снова и снова. Я слы­шал, что Дюбуа-Реймон заметил это же явление, сравнивая степени роста функций, и это привело его к удивительному выводу, что нет окончательно­го критерия сходимости рядов, который был бы универсальным.

Континуум. Это второй столп, на котором стоит математика. Одна­ко, в отличие от множества, его математический характер не совсем по­нятен не только мне, но и Дедекинду, хотя мы и дали ему арифметическое описание. Сам Аристотель не допускал возможности рассматривать кон­тинуум как множество, хотя позже это использовал Ньютон для основания Евдоксовых пропорций, упорядоченных в соответствии с их геометриче­ским разложением. Тем не менее и в наши дни большинство математиков рассматривают континуум скорее как геометрический или даже физиче­ский объект. Некоторые свойства, постулированные Гауссом, достаточны, чтобы строго пользоваться ими в математических рассуждениях. По Гауссу, нет необходимости рассматривать их как объект, построенный с использо­ванием более первичных понятий.

Опираясь на эти геометрические и физические мотивации, мы долж­ны думать, что континуум скорее истолковывался нами, а не конструиро­вался. Например, мы при этом объясняем, как заполнить пробелы, и это было известно со времён Ньютона или даже со времён Евдокса. Мы сдела­ли конструкцию, и по существу неважно каким образом.

———————-· ————————————

Рисунок 1. Континуум

Хотя Дедекинд и соглашается часто с этой скромной точкой зрения, но он говорит, что мы можем рассматривать нашу конструкцию безотноси­тельно к физической или геометрической интерпретации. Сначала мы мо­жем рассматривать дроби как создание наших мыслей, как упорядоченные пары натуральных чисел, отвлекаясь от общих факторов. Позже мы можем работать с ними только как с логическими абстракциями. По-моему, эти логические абстракции являются классами дробных последовательностей. Пополнив множество дробей этими абстракциями и расширив порядок, мы получим упорядоченное множество без лакун, тогда объект будет упо­рядочен как физическое твёрдое тело. Независимо от того, насколько сложна эта конструкция, здесь для этого используются только числа, мно­жества и логика.

В беседах я много раз обращался к вышеупомянутой аргументации. Те­перь я чувствую её некоторую несостоятельность. Дроби m/n и p/q  счита­ются равными, если mq = np, но здесь учитывается физический смысл связи с весом тел. В чисто арифметическом смысле мы должны уделять внимание делимости. Кроме того, расстояние m/n-p/q означает близость в геометрическом и даже физическом смысле. Таким образом, в наших построениях мы не свободны от физических и геометрических смыслов, по крайней мере, в интерпретации. Таким образом, континуум не входит в сферу чи­стых множеств.

Чистые множества. Я часто говорю, что для того, чтобы получить множество, которое я называю чистым, нужно, имея конкретное множе­ство, абстрагироваться прежде всего от природы его элементов, и затем от его структуры. Например, от его упорядоченности.

Однако в этом предположении есть некоторые трудности. Мы окажем­ся перед призраками мёртвых множеств! Их элементами будут лишь тени прошлого. Помнят ли они своё предыдущее состояние? Но давайте оставим эти кошмары, это всё-таки множества, бывшие призраками яблок и груш. Даже величайшие философы не осудят этой неопределённой ситуации.

Допустим, что элементы чистого множества выглядят, как белые биле­тики, которые неразличимы между собой. Это противоречило бы взгляду Лейбница на случай более, чем одного белого билета, но белые билеты действительно существуют. Кроме того, существует много совокупностей, элементы которых неразличимы в первый момент, но они становятся раз­личимыми в процессе рассуждения. Так что пренебрежём сомнениями Лейбница. Наш разум способен воспринимать точку как пятнышко, кото­рое разделяется на два пятнышка, каждое из которых неотличимо от другого и от материнского пятнышка. Продолжая этот процесс, мы можем полу­чить в качестве примера множество как чистое создание нашего разума, природа элементов которого незначима для дальнейших целей.

Посмотрите на числа. Как бы мы их ни обозначили, это не помешает нам считать. Нам нетрудно перемножить их или поделить. Однако заметим, что математика не указывает нам, когда нужно умножать или делить. Это общая проблема применимости и мы можем пренебрегать ею в изучении чистых множеств.

Следующая абстракция, именуемая абстракцией структуры, более существенна. Если фигура имеет форму, некоторые места её могут тракто­ваться как точки или символы, обозначающие положение этого места на рисунке. Напомним наблюдение Евклида, что «прямая линия есть та, ко­торая равно лежит во всех своих точках» («Εὐθεῖα γραμμή ἐστιν, ἥτις ἐξ ἴσου τοῖς ἐφ’ ἑαυτῆς σημείοις κεῖται»). Было ли это той причиной, по которой Евклид не воспринимал линию как множество точек?

Но я не отвергаю идею чистых множеств, даже лишённых какой-ли­бо структуры. Множество белых билетиков — это объект наших мыслей, поэтому мы должны приложить усилия для их изучения.

Встреча в Интерлакене. Мы встретились случайно: «Профес­сор Дедекинд, я полагаю?» — что-то в этом роде. Это была встреча двух теорий иррациональных чисел. Дедекинд воистину гордился своей теори­ей, которая в точности соответствовала ожиданиям Античности. Она по­зволяет кратко и строго доказать, что квадратный корень из двух, взятый кратно квадратному корню из 3, будет равен квадратному корню из 6, ска­зал он. Он рассказывал, что эта идея пришла ему в голову во время его лек­ции в Политехническом университете в Цюрихе. Он помнил, что это было 25 ноября 1858 года⁵. Я знаю эту дату из брошюры, и я удивлялся, почему он не добавил, что это произошло в 9 часов утра. Он сказал, что приготовил эту конструкцию только как интересное упражнение, и что он всё время откладывал её публикацию, пока в прошлом году не была опубликована те­ория вещественных чисел Коссака. Он не придал ей большого значения как лишённой математического духа и красоты. Для меня не секрет, что Деде­кинд не любит берлинцев, и что теория фактически принадлежит Вейерш- трассу. Моя теория была им принята доброжелательно. Эту теорию следо­вало бы разработать Коши, сказал он, но Коши опасался высоких уровней абстракции и оказался в порочном круге, когда определял действительное число. Наши континуумы эквивалентны упорядоченным множествам, ко­торые должны обладать свойством непрерывности в отношении порядка, сказал он, и как раз этот смысл придан слову «непрерывность» в назва­нии его брошюры. Благодаря этому свойству построенный объект может быть назван линией. Значимость непрерывности линии была также отме­чена Больцано в его строгом доказательстве «Zwischenwertsatz» (Теорема о среднем).

Трудно сказать, что я говорил Дедекинду. В основном говорил он. Он относился ко мне как к новичку. «Пожалуйста, напишите мне о Ваших раз­мышлениях», — сказал он мне на прощанье.

Дедекинд — один из нашей большой четвёрки. Встреча с ним развеяла моё одиночество, ощущаемое в Галле, когда моя работа по тригонометри­ческим рядам была завершена. Несколько моих студенческих лет прошло в Цюрихе, но как раз в те годы Дедекинд вернулся в Брауншвейг заведовать кафедрой математики, которую ему предложили в Политехническом, пре­образованном из прежнего Каролинума.

Скромное начало. Ничего странного в том, что Дедекинд не был удивлён моим замечанием в духе Галилея, что дроби могут выглядеть как последовательности. Это может быть сделано несколькими способами.

Его гораздо больше заинтересовало моё доказательство о точках пря­мой. В ответ он прислал мне своё доказательство, почти повторяющее моё. Непрерывность в отношении порядка играет решающую роль в наших до­казательствах. Аргументация подобна той, которую я использовал в своём доказательстве о коэффициентах тригонометрических рядов. Прислав мне своё доказательство, Дедекинд лишил меня чувства удовлетворения от мо­его открытия. Является ли это его недостатком? Могу ли я утверждать, что он перенял его у Гаусса, который не смог быть щедрым к молодому Бойяи? Была ли известна ему эта проблема и доказательство до меня? Я не могу этого исключать, наслышан о его «Treppenverstand», о его медлительном уме, в чём он с улыбкой сознавался.

Я признаю, что его доказательство немного проще. Должен ли я побла­годарить его за это? Это поставило бы нас обоих в неловкое положение. И, кстати, его доказательство фактически такое же, как моё.

Доказательство. Возьмём точки а₁ а₂,,… на прямой. Пусть интервал I₁ не содержит а₁ интервал I₂, не содержит а₂ и лежит вместе со своими кон­цевыми точками на I₂ . И так далее. Общей точкой всех этих интервалов, существование которой гарантируется непрерывностью, будет точка, отличная от всех рассматриваемых точек а_n.

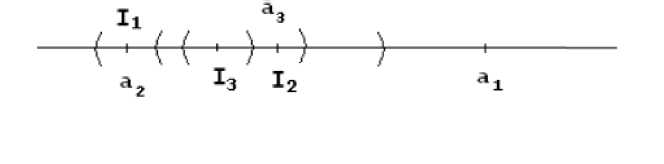
Я хотел бы отметить, что в этом доказательстве я обращаюсь к матема­тически конкретным множествам, к обоснованию через геометрический смысл, даже через физический. Удалось ли бы мне найти подходящие сред­ства, если бы я обратился к множествам без всякой структуры?

Дедекинд настоял, что мой результат стоит публиковать с коммен­тарием, что множество алгебраических чисел счётно, доказательство чего подобно моему доказательству о счётности множества дробей. Оба этих утверждения допускают существование трансцендентных чисел.

Не изобрёл ли я того, что было сделано Лиувиллем? Без всякого упо­минания трансцендентных чисел? Это какой-то замкнутый круг, когда я доказываю существование чисел, которые были созданы мною самим. Мне стало страшно, и сердце моё забилось.

Крик беотийцев. Почему Гаусс так опасался криков беотийцев? Мате­матики составляют сообщество, подобно ордену. Хотя законы не писаны, но профессиональный канон известен ещё с античности, не предполагая отступничества, этот пифагорейский принцип был силён до наших дней. Предмет, из которого появляются результаты, должен быть прочным. Это­го придерживался Гаусс. Он создавал свои работы из чисел, не доступных профанам, которым ничего не оставалось. Как не преклоняться перед ним? Другой его любовью была геометрия, связанная с геодезией и физикой. Он сказал там первое и последнее слово. Он занимался вещами высшей важно­сти, что обеспечило ему первенство в математике. Многие его результаты остались в мелких заметках. Он пользовался узлами, но исследование тео­рии оставил Листингу. Он считал тратой времени писать монографии, как Коши с его тщательной кодификацией понятий производной, интеграла, непрерывности. Но оборотной стороной его почёта было одиночество.

Будучи открывателем «Превосходной теоремы» (Theorema egregium), он, как никто другой, в то время продвинулся в решении проблемы по­стулата параллельных Евклида. Но он не решался обсуждать эту пробле­му с беотийцами, которые знали этот вопрос в упрощённо-вульгарной форме. Может быть, он имел в виду Ньютона, чья грандиозная идея о вос­становлении изменяющейся величины по её интенсивности изменения была сокращена для профанов в dy/dx`на века лишив математику красоты.

Беотийцы — как их много вокруг меня — примут мои множества в про­стейшей форме. Позже, освоив мою идею, они станут меня исправлять. Не ошибся ли я, показав мою идею сразу после её создания?

Кронекер и берлинцы. Хотя моя статья принята в журнале Крелле, я не могу избавиться от беспокойства. Несомненно, в Берлине следят за мной. Независимо от того, какое положение Дедекинд занимает в Брауншвейге, он берлинец до мозга костей. Я слышал, что самое плохое мнение о моём интересе к теории множеств высказал Кронекер. Я чувствовал острую го­речь, ибо я был близок с ним в Берлине и он по-дружески относился ко мне. Он фанатик арифметизации, но на классический манер. По его мне­нию, числа первичны по отношению к другим математическим понятиям. Истолкование их в других терминах было бы святотатством. Однако он отнёсся равнодушно к рассуждениям Коссака. Он проглотил эту горькую пилюлю, успокоенный Вейерштрассом, что это сделано только для боль­шей строгости. Хотя Дедекинд стоял в стороне от наших арифметических построений как завершающего истинного шага к арифметизации матема­тики, он был убеждён, что арифметические методы неуместны в основных разделах геометрии. Арифметизация — это не более чем мысленное до­пущение для того, чтобы всё сосчитать и упорядочить. Между тем анализ был схоластичен с самого начала, в качестве основания его математическо­го статуса годился физический континуум, хотя мы знаем, что лишь наша арифметизация превратила правдивые постулаты Ньютона в теоремы, са­мая важная среди которых: если f’= 0, тогда f= const.

Все математики Берлина принадлежат к направлению геттингенских алгебраистов, из которого вышли Гаусс и Дирихле. Хотя я не слышу их кри­тики в свой адрес, но их безразличие удручает меня. Они относятся к моей математике как к маргинальной и снисходительно оценивают её как без­обидное крючкотворство (Spitzfindigkeiten).

Алгебраическая теория чисел, начало которой положил Гаусс, и из­вестная мне по «11 Дополнению» Дедекинда, в работах Кронекера и Кум- мера поднялась на чрезвычайно высокий уровень абстракции. Понятие делимости чисел и свойство быть простым числом должно быть определе­но заново. Идеальные элементы были введены ради сохранения принципа разложения на простые множители. Я преклоняюсь перед этими великими математиками.

Я один со своими чистыми множествами. Я отложил мои исследова­ния тригонометрических рядов. Для моих коллег было неожиданностью, что сходимость ряда на произвольно малом интервале позволяет сделать вывод о сходимости к нулю коэффициентов. Это позволило мне проник­нуть в суть рассуждений Римана и Амандуса Шварца и, наконец, получить теорему единственности тригонометрического разложения. Должен доба­вить, что об этой работе тепло отозвался Кронекер. И теперь как блудный сын я чувствую его укоризненный взгляд.

Плоскость и прямая. Я быстро получил ответ от Дедекинда по поводу моего доказательства того, что множество точек прямой и плоско­сти находятся во взаимно-однозначном соответствии. Он расценил этот результат как интересный, но его дотошные вопросы были невыносимы. Перегруппировывая десятичные представления координат х и у точки р на плоскости, я получаю точку f(p) на прямой. Преобразование f очевидно взаимно-однозначно. Но Дедекинд заметил, что на прямой не все точки могут быть значениями f. Он указал такие точки на прямой, которые име­ют в своём десятичном представлении в качестве альтернативы цифру О, и напомнил мне, что я заранее исключил представления, заканчивающиеся нулями. Я был расстроен моим недосмотром.

Пока я убеждён, что я доказал даже больше, чем равносильность пря­мой и плоскости, потому что я установил равносильность плоскости и ча­сти прямой! Из этого факта равносильность между плоскостью и прямой следует непосредственно, имея в виду, что прямая — это часть плоскости. Но справедливость этого закона неочевидна.

Тем же вечером я послал Дедекинду доказательство, основанное на пе­регруппировке разложений непрерывных дробей, которое позволяет без исключений обеспечить единственность представления в области ирраци­ональных чисел. Я получил соответствие между множеством иррациональ­ных чисел и множеством пар иррациональных чисел. Этого достаточно для получения предыдущего результата, так как множество иррациональных чисел равносильно всему множеству действительных чисел, ибо они отли­чаются лишь на счётное множество рациональных чисел.

Однако это доказательство было несколько неуклюжим. Я доказывал это разными способами, но все они казались мне далёкими от математиче­ского совершенства. Наконец я свёл трудности к рассуждениям, подобным рассуждениям о равносильности между отрезком и отрезком с изъятой точкой. Дедекинд одобрил мои соображения, обрадовавшись, что доказа­тельство после всех изменений выглядело удовлетворительно.

Хотя я и не был совершенно удовлетворён моим доказательством, всё же я ожидал от Дедекинда большего внимания и дружелюбия. Вместо этого я услышал несколько хладнокровных советов, почти что предостережений, главным образом против связи моих результатов с размерностью, для ко­торой взаимно-однозначное соответствие неуместно, если оно не являет­ся непрерывным. Я согласился с этим замечанием, мне было всегда ясно, что соответствие, основанное на перегруппировке цифр, полученное про­извольным образом, далеко от непрерывности. Однако было в этом ком­ментарии что-то холодно-отстранённое. Но вновь взглянув на это письмо, я нашёл там много вежливых слов и выражений, которые едва ли можно было назвать равнодушными, скорее, они были советами.

Дедекинд крайне беспристрастен в своих суждениях, распознавая зна­чимость математического результата независимо от сочувствия. Он дал мне совет быть подальше от философии. Он расценивает философию ма­тематики как область своих интересов. Что, как не философия, изложено в его книге «Что такое числа и для чего они служат?», — книге, которую он создавал в своих мыслях многие годы по правилам, известным только ему? «Оставь, пожалуйста, философию грекам», — посоветовал он мне в одном из писем.

Теорема, которая должна быть доказана. Я не удовлетворён моими доказательствами, которые кажутся мне второстепенными. Они относятся к множествам, математически готовым. Смогу ли я приложить их к множе­ствам, которые я называю чистыми множествами?

Я вернулся к моему первому доказательству о равносильности плоско­сти и прямой. Я показал, что плоскость может быть представлена равно­сильной подмножеству прямой. Но, с другой стороны, прямая содержится в плоскости. В общем случае должно быть верно, что если множество В содержится во множестве А, и множество А находится во взаимно-одно­значном соответствии с подмножеством В, значит, между А и В существу­ет взаимно-однозначное соответствие. Похоже, что это общий закон те­ории множеств, фактически теории чистых множеств. Но в теории чистых множеств ни правила, ни гипотезы не доказаны. Я вижу, что сформулиро­ванная как теорема моей теории это первая явная теорема теории чистых множеств.

Почти три месяца я ждал письма из журнала Крелле. Я спрашивал Деде – кинда, что было причиной задержки. Его ответ был уклончивым. Возмож­но, задержка была вызвана трудностью оценки результата. Тогда я спросил его, стоит ли опубликовать результат отдельной работой, но он посовето­вал набраться терпения.

Эта статья в конце концов была опубликована, я беспокоился. Вейерштрасс одобрил её, хотя может быть и не без колебаний.

В тени Дедекинда. Письма Дедекинда стали нелюбезными. Факти­чески он предостерегал меня против злоупотребления понятием размер­ности. Это было неверное представление. Для меня всегда было ясно, что в вопросе о взаимно-однозначном соответствии основой является непре­рывность. Когда я послал ему своё доказательство невозможности непре­рывного взаимно-однозначного соответствия между пространствами раз­личной размерности, его ответ был ответом типичного школьного учителя, который с внимательным наслаждением отслеживает мельчайшие ошибки своего ученика, даже самые незначительные из них. Я потерял желание обмениваться с ним идеями. Сравнивать наши позиции как конкурентные было бы смешным. Я бы скорее допустил, что он всегда неприязненно от­носился к моим интересам к бесконечности. Он рассматривал их как не­серьёзные игры. С другой стороны, я вижу, что эта холодная реакция могла быть следствием его характера и, возможно, не относится ко мне лично, равно как и к сущности вопроса.

Теперь я намерен дальше заниматься актуальной бесконечностью, но я потерял желание сотрудничать с ним. Думаю, что это опустошило бы меня. Даже при всём его терпении я бы чувствовал себя зависимым от него. Даже достигшая меня критика Кронекера не так подавляла, как холодные вежли­вые письма Дедекинда. Я должен выйти из его тени. Мне нужно найти свой собственный путь в математике.

Последний обмен письмами с ним по поводу невозможности непре­рывного взаимно-однозначного соответствия между евклидовыми про­странствами Е^m и Еⁿ если m и n различны, был мучителен. Доказатель­ство проводится индукцией по отношению к т и п . Дедекинд прицепился к небольшому упущению в описании второстепенного отображения, ко­торое не определено в конечном, возможно, счётном количестве точек, не желая видеть, что это упущение легко восполнить.

Я знаю, что у него в голове своё доказательство, и он об этом перепи­сывается с Томе и Нетто, возлагая надежды на хорошую идею Нетто. Вот почему я послал моё доказательство в «Göttinger Nachrichten», не дожида­ясь одобрения Дедекинда⁶.

Превращение старого мудреца. Он стареет, хотя ему нет и пятидеся­ти. Кто-то сказало нём: «das ewige Misantroph» (вечный мизантроп). Ему ничего не надо, кроме родного Брауншвейга и отцовской виллы. Он откло­нил приглашение в Галле, так как его амбициям соответствует только Бер­лин. Но сейчас даже Берлин неприятен ему из-за окружившей его с годами возрастающей атмосферы враждебности. Он чувствовал себя мудрее всех берлинцев, хотя шёл к этому годами, никогда не первенствуя. В Гёттингене он был в тени великих наследников Гаусса, прежде всего Дирихле, а затем Римана, а теперь он подавлен шумом вокруг Кронекера и прославлением Вейерштрасса, который стал вроде математического божества. Мы читаем о трагической судьбе юных гениев, но и судьба стареющего учёного тра­гична. Брауншвейг — это наша Беотия. Оттуда не появляется ничего зна­чительного. Он равноудалён от Берлина и Гёттингена, а также от Гамбурга и Галле. Прославится ли он как город Дедекинда? Нет! Потому что здесь родился Гаусс и здесь ему воздвигнут памятник! Возможно, даже Гаусс чув­ствовал себя здесь беотийцем из-за трудных детских школьных лет. Была ли Беотия реальным пророчеством утраты радости жизни? Однако рядом с Брауншвейгом были пологие горы Гарца и чарующий Гарцбург. Нельзя упустить и поэтический Веймар, где проживал Гёте. Горькой правдой было то, что Гёте никогда не приглашал Гаусса к себе, игнорируя его большую славу. Гаусс часто бывал в Веймаре, заезжая в Вену для покупки там стёкол для своих инструментов⁷.

Серое вещество множеств. Целью моей «Mannigfaltigkeitslehre» (Уче­ние о множествах) было продолжение моей детской мечты о расширении понятия числа за пределы натуральных чисел. Но до того как я приложил много усилий к изучению множеств, лежащих на прямой, у меня был инте­рес к ним самим, как к предмету дальнейших исследований. Я занялся этим, чтобы сделать мою теорию самодостаточной. Я с трудом преодолел обыч­ные свойства, доступные даже новичкам, связанные с описанием положе­ния точки на прямой. Точки могут быть изолированы, но могут сгущаться. Я освоил эти понятия, когда работал над тригонометрическими рядами. Но теперь я должен систематизировать все детали.

Однако среди этих мелочей были и исключения. Это множества, кото­рые получаются из интервала после удаления открытых взаимно не касаю­щихся подинтервалов так, что не остаётся ни одного полного подинтервала, ни изолированных точек. Неважно, насколько малым окажется такое мно­жество в смысле его протяжённости, оно останется во взаимно-однознач­ном соответствии ко всему интервалу. Я нашёл хорошую арифметическую формулу, описывающую одно из таких множеств⁸. Однако мне стало извест­но, что такие множества знакомы тем, кто занимается теорией интеграла.

Все ли множества на прямой, исключая конечные множества и после­довательности, эквивалентны всей прямой?

Исследуя подмножества прямой, я обнаружил, что все основные труд­ности преодолимы. Хотя я не ощущаю себя полноценным математиком. Здесь я чувствую себя сухим серым веществом. Какая разница в сравнении с живой материей тригонометрических рядов! Они вкраплены в царство арифметики, поддерживаемые ритмом, с каждым шагом получаемым от чи­сел. Для Кронекера, которому я так многим обязан, числа — это бьющееся сердце математики. Снимаю перед ним шляпу. Я понимаю, будучи матема­тиком старого образца, он должен быть против теории множеств. Он весь как на ладони со своей критикой, не скрывая её от меня в наших беседах. Я бы сравнил его с шевалье де Мере, известным своей неприязнью к Блезу Паскалю. Кронекер — старший из нашей великой четвёрки.

Мной завладела далёкая от ежедневной рутины идея трансфинитного, и я вновь написал Дедекинду о своей идее трансфинитных чисел. Но ответа не получил.

К свободе математики. Дедекинд отметил очевидное свойство на­туральных чисел, что в каждом их множестве есть наименьший элемент. Я вижу, что мои последовательности символов 1, 2,…, ω, ω+1, ω+2,… тоже обладают этим свойством. Поэтому я не вижу препятствий назвать мои символы числами. Для каких целей они служат? У меня есть одна идея на­счёт этого. Но ведь они и в самом деле существуют! Они принадлежат математике, как и другие вещи, созданные нашим умом и свободные от противоречий. Математика в своём развитии не прогнозирует барьеров. Сущность математики в её свободе, и я не обязан давать объяснения от­носительно применимости моей новой системы чисел. Сейчас, работая над своим «Мемуаром», я посвящу несколько страниц изложению моих убеж­дений о свободной математике⁹.

Как бы восприняли меня коллеги-математики в роли философа или даже пророка? Математики таких не любят и даже чураются. Может быть, лучше сначала опубликовать краткие результаты, подождать и посмотреть, как они отреагируют. После любой публикации люди будут искать изъян, чтобы полностью дискредитировать сделанную работу. С другой стороны, я чувствую необходимость проявить свои убеждения, которые я так долго скрывал.

Однако даже в этой свободной математике я не чувствую такой сво­боды, какой ожидал раньше. Подъём по моей числовой лестнице был на­стоящим математическим предвидением. Выбирая возможное решение, я обнаружил столько необходимых условий, что результат определился однозначно. Где вожделенное удовлетворение, которое должно сопрово­ждать свободное творчество? Мы способны обнаружить только уже суще­ствующие формы!

Но тогда у меня было лишь смутное представление о них. Расширен­ный ряд чисел в некотором смысле подчиняется известным законам мно­жества целых чисел, а именно, он вполне упорядочен. Не вдаваясь в деталь­ное определение, заметим, что для двух вполне упорядоченных множеств, одно из которых подобно начальному сегменту другого, никакое из них не подобно никакому своему собственному начальному сегменту. Однако прибавление нового элемента не влияет на увеличение количественного размера совокупности. Множества, которые я получал на первых этапах довольно длинной процедуры, всегда были равносильны множеству целых чисел. Но тут возникает более существенный вопрос: могу ли я рассматри­вать эти совокупности как формализованные логические сущности и могу ли я называть их множествами? В таком случае это зависит от моего соб­ственного решения! Ну и какова же будет для научного сообщества цен­ность моего чистого творения?

Я не свободен от этих сомнений даже у себя дома. В моих записях, от­крытых моим гостям, не встречаются ни знаки интеграла, ни суммирования рядов. Для равновесия я написал статью по алгебраическим числам. В на­дежде, что её прокомментирует Дедекинд, но этого не случилось. Вижу, как моё неловкое молчание и беспричинные всплески раздражения тяготят Гертруду и Эльзу.

Моя болезнь — приходится использовать это слово — заключается в том, что я вижу всё в серых тонах. Множества вне математического кон­текста лишены также энергии, напрягающей мышление, я помню это со времён работы над тригонометрическими рядами и моих ранних работ, по­свящённым числам. Я чувствую, что главный источник депрессии — мно­жества на многообразиях. Они бесформенны, неупорядочены и практиче­ски обезличены. Только сильное раздражение способно освободить меня от мрачных мыслей. Такой полный раздражения очерк я написал по поводу книги Фреге. Я написал, что понятие числа не может быть сведено к обще­му свойству множеств быть эквивалентными друг другу. Это никудышная или временная замена. Числа должны быть определены раньше, и един­ственно возможный способ получить их — это различие между порядко­выми числами.

Я стараюсь остановить свои эмоции. Я ожидал, что переписка с Его Преосвященством будет достаточной для этой цели, но я разочарован. Бо­гословы думают, что среди моих чисел проходит дорога в рай. Они живут в параллельном мире.

Вполне упорядоченная шкала. Мои числа едва образуют совокуп­ность. Как я утверждал с самого начала, совокупность элементов может рассматриваться как множество, если есть идея, которая описывает их как вполне сформированное единство, что позволяет решить, является дан­ная вещь членом совокупности или нет. Хотя это нечёткое условие вполне достаточно для совокупностей из математических контекстов, но в случае моего чистого множества порождает серьёзную проблему. Совокупность моих чисел ни в коем случае не может рассматриваться как абстракция из множеств, которые уже сформированы в математике, в частности, вроде тех белых билетиков, которые я ещё готов допустить. Они вводятся индук­тивно, каждое новое множество создаётся из элементов ранее созданного множества. Согласована ли эта итеративная процедура с моим прежним ут­верждением о формировании множеств? Ситуация несколько прояснится, когда я рассмотрю множество всех тех моих символов, для которых множе­ство их предшествующих элементов счётно. Такая совокупность хорошо представима, поэтому я решил рассмотреть её как множество. Я называю его множеством трансфинитных чисел II класса. Я доказал, что оно несчёт­но. В отсутствие этого утверждения мы должны считать, что оно было бы одним из своих собственных сегментов, что невозможно для вполне упо­рядоченного множества.

Обозначим символом ω₁  трансфинитное число, соответствующее II классу. Это первое несчётное в этом смысле число.

Эквивалентно ли множество чисел II класса множеству точек конти­нуума? Этот вопрос естественно встаёт, но, с другой стороны, он выглядит экзотически, так как эти множества принадлежат различным математиче­ским контекстам!

И снова континуум. Я вновь обратился к моей первой беседе с Деде- киндом о физическом характере континуума. После этой беседы я выска­зал свои сомнения о возможности включить континуум в систему основных понятий, основанных лишь на числах и множествах. Теперь вопрос выгля­дит так: можно ли вполне упорядочить континуум, итеративно исчерпывая его точка за точкой. Независимо от того, насколько тщательно это выпол­нено, это упорядочение не будет связано с естественным, плотным в себе, геометрическим упорядочением.

Я считаю арифметический континуум пробным камнем моей теории. По правде говоря, континуум формально не принадлежит моей теории. В теории чистых множеств, особенно в идее трансфинитного, он является посторонним и чуждым. Он проник в платоническую математику с чёрного хода из области практических обмеров полей в долине Нила. Тем не менее математика признала факт его существования. Да и ничто не препятствует рассматривать его как множество. Это было установлено вопреки Аристо­телю мной и Дедекиндом!

Всё ещё не нашла объяснения знаменитая старая апория Зенона о ле­тящей стреле. Наше описание статично и неуместно для движущейся переменной. Но оставим этот вопрос и обратимся к огромному много­образию подмножеств континуума. Я уже упоминал о той гипотезе, что бесконечные подмножества континуума, неэквивалентные целым числам, будут эквивалентны всему континууму. Это справедливо для множества иррациональных чисел и даже для некоторых множеств, которые неплот­но расположены в континууме. Однако моим поискам ещё далеко до за­вершения. Это предположение будет подтверждено, если окажется, что континуум эквивалентен множеству трансфинитных чисел II класса, ибо для них справедливо это утверждение.

Пока меня неотступно преследуют несколько общих вопросов. Есть ли другие множества кроме тех, которые являются подмножествами контину­ума? Трудно поверить, что континуум служит универсальным вместилищем множеств. Если это так, он должен быть обширным, как мир наших мыслей. Но что мы имеем в виду, когда говорим произвольное множество? Сто лет назад Эйлер и Даламбер спорили о понятии произвольной функции.

Миттаг-Леффлёр. Я узнал, что в центре интересов теории функций лежат сингулярные множества прямой и плоскости. Сингулярности анали­тических функций не обязательно будут изолированными, они могут нака­пливаться в точках и даже образовывать континуумы. Густав Миттаг-Леф­флёр, который за последнее время стал весьма известен, сделал небольшую ошибку в обосновании доказательства сгущения точек. Я послал ему свои критические замечания. Он ответил очень вежливо. Написал, что читал мои статьи, ими заинтересовались и его шведские коллеги. Миттаг-Леф­флёр учился в Берлине у Вейерштрасса. Недавно он основал в Стокгольме очень престижный журнал «Acta Mathematica». Весь прошлый год он про­вёл во Франции.

Ободрённый, я послал ему статью о сингулярностях множеств прямой, плоскости и других многообразий в «Acta», зеркало его интересов. Он бо­гатый человек, обаятельный и энергичный в организации математической жизни, пользующийся влиянием в Берлине. Софья Ковалевская благодаря ему получила veniam legendi (право читать лекции) в Стокгольме.

Месяц за месяцем наша переписка стала систематической. Из его пи­сем я узнавал математические новости. Мы обменивались мнениями, имея общую точку зрения на взгляды Кронекера. Я понимал, что его критика не была прямо связана с моими последними результатами о трансфинитном. В анализе не упоминается трансфинитное, но любопытны некоторые пре­дельные множества. Я узнал от него, что моя теорема о разложении мно­жества на два, одно из которых плотно в себе, а другое счётно, была также получена его коллегой Бендиксоном, и что Фрагмен в Финляндии полу­чил важные результаты о множествах, которые не могут разъединить пло­скость. Отныне я стал спокойнее воспринимать такие новости. Я чувствую, что я не одинок в своём увлечении множествами.

Однако далеко не математика была главной в наших письмах. В них я по­лучил возможность выразить мою точку зрения. В ответ я получал ободря­ющие слова и тёплое признание моей идеи трансфинитного. Я согласился с предложением Миттаг-Леффлёра опубликовать в «Acta» французский перевод моих предыдущих статей, в частности, «Linear Mannigfaltigkeiten».

«Versöhnungbrief» (послание о мире) Кронекеру. Это не Кронекер¹⁰, а я сам послужил причиной рокового состояния моего здоровья. Это моя вина, что я без слов оставил наши общие интересы в теории рядов. Он был моим наставником, и я чувствую себя перед ним блудным сыном. Моя пе­реписка с Миттаг-Леффлёром стала бессодержательной, начала тяготить меня. Не скажу, что я чувствую холод, но и тепла в наших отношениях не стало, просто ровный обмен комплиментами, как во время его последнего посещения Галле. Он во многом согласен со мной. Я понимаю, что он про­тив берлинцев, которые, одобрив Фуса (Fuchs), закрыли перед ним дверь. Он болтает о пустяках, но ничего не говорит о моих статьях, посланных ему в «Acta».

Между тем Кронекер, который открыто объявил о своём несогласии с моими множествами, говорил со мной честно и искренне. В спорах он никогда не был пренебрежителен ко мне. Я узнал, что он готовит полеми­ческую статью в «Acta». Однако при моём теперешнем состоянии здоровья я не способен вести публичные диспуты. Я решил написать моему старо­му профессору письмо, выражающее мои истинные взгляды и чувства.

Ответ Кронекера. Я не ожидал такого проявления внимания от Кро- некера, его ответ в самом деле был искренним и дружелюбным. Он написал, что действительно не согласен с моими взглядами, но мы должны отстаивать их. Я был тронут его предостережением в конце письма. Он написал, что в математике не нужно создавать новые понятия. Они для него на заднем плане. В математике имеют высшую ценность только конкретные струк­туры, и заключаются они в формулах. Только формулы — как знаем мы из истории — только формулы бессмертны!

Я узнаю здесь свою мысль, многократно появлявшуюся у меня. Но каж­дый из нас выбирает свой путь в математике, часто случайно. Послужил ли тому случай в Интерлакене? Наш путь в математике проходит уникурсаль- но, прошлое не повторяется. Не только мы, математики, подчиняемся этим грубым законам, но и сама математика тоже. Эти мысли могут показаться пессимистическими, но я, как никогда раньше чувствую покой и уверен­ность, внутренние сомнения оставили меня. Я благодарен Кронекеру за его мудрые правдивые слова.

Ответ Миттаг-Леффлёра. Я ожидал этого. Письмо начинается с обычных комплиментов. Он высоко ценит мои идеи, но признаёт, что не все математики придерживаются таких же взглядов. Затем после несколь­ких пустых слов, впадая в менторский тон, он советует завершить статью конкретными выводами, не считаясь с тем, как важны идеи, содержащи­еся в моей статье. И, наконец, он мягко предлагает опубликовать резуль­таты в форме отдельной статьи. В ответ я отозвал свою статью из «Acta».

Я понял, что наша дружба закончилась. Была ли это в самом деле дружба? Можно ли употреблять это слово, если отношения не выходили за рамки знакомства с некоторой долей учтивости? Но более всего удручает меня то, что я согласен с его комментариями. Безнадёжность моих усилий в под­тверждении гипотезы континуума вынуждает меня согласиться с ним.

Средства, которые я приготовил для получения моей обещанной те­оремы, например, несколько лемм об упорядоченных множествах, потре­бовали от меня огромной работы, но оказались бесполезными. Я потерял веру в то, что арифметический континуум займёт своё место на моей шка­ле трансфинитных чисел. Но представьте себе, что я действительно полу­чил свою долгожданную теорему и послал её в «Acta». Мог ли я ожидать от Миттаг-Леффлёра нечто большее, чем любезные слова: «Благодарю Вас за интересный результат»? Видимо, ему чужд опыт математики. Какое отли­чие от меня и от Дедекинда!

Пушкин. Я помню, как мой отец говорил о Пушкине. Мы приехали сюда из Петербурга, где все имеют собственное мнение по поводу спора известного поэта с не менее известным здешним шевалье де Мере. По об­щему мнению, ни шевалье де Мере, ни Император не несут ответственно­сти за судьбу Пушкина, кроме него самого. Людям кажется, что некоторая безнравственность двора — вещь обычная, даже неотъемлемая для такого места. Но не для Пушкина. Он жил в своём собственном мире. Его беда в том, что он неспособен был переносить малейшую фальшь.

Таков ли мой характер, как у Пушкина? На что я надеялся, ожидая, что мои трансфинитные числа с энтузиазмом примут в журнале Крелле? По­чему я жду, что Нетто посвятит мне более двух фраз в своём обзоре? Мои коллеги не избалованы хорошими неожиданными цитированиями. С дру­гой стороны, известность некоторых людей в большинстве случаев основа­на на фальши. Мне не ясно, почему Вейерштрасс настоящий лидер. Равно­мерную непрерывность открыли Зейдель и Гудерман. А Гейне исследовал возможность почленного интегрирования.

Мог ли Пушкин чувствовать себя лидером? Он писал: «Я памятник воздвиг себе…». Здесь он был прав. Часто почёт приходит после смерти, цена ему невысока. Но он был осуждён за то, что в своих стихах выражал суждения от имени всего народа. Не слишком ли много брал он на себя как сочинитель? Остроты — это привилегия придворных шутников. Как Ми­нотавр, Пушкин должен был видеть себя в двойной роли, видя себя в зерка­ле собственных мыслей и в чуждом отражённом свете. Шумный вздох царя, молодой повеса-капитан, тишина в зале, улыбка Натали и другие мелочи утомляли его. Чтобы прогнать тёмные мысли, он вёл себя как герой даже в обыденных ситуациях. Хотя его внутренний мир отражал не только сти­хи, написанные им самим. Были безделицы, вписанные в альбомы очарова­тельных дам, были сатиры, которые заведомо не могли быть опубликованы.

В одну из таких тяжёлых минут он услышал хорошо знакомый шёпот… Ему было известно, что его дед приехал из Эфиопии, сопровождая Царя царей, и гордился им. Его дед не был здесь чужим. А внук стал изгоем!

Эти слова о Пушкине так правдивы, что их не нужно комментировать. Но что роднит меня с последним высказыванием? Мой дед приехал из Ко­пенгагена в Петербург, где родился мой отец, и был крещён в лютеранскую веру.

Я никогда не придавал значения истории своей жизни, меня никогда о ней не расспрашивали ни в Петербурге, ни здесь. Однако люди говорят, что дело совсем не в этом.

Можно ли понять новое? Юный Феликс Клейн, ныне известный, вы­сказался несвойственно университетскому сообществу. Он сказал, что ха­рактер математики зависит от духа нации. Я согласен, что наши математики воспитаны по Гауссу, становясь более концептуальными и свободными от французской вычислительной традиции. Но я не могу согласиться с упро­щённостью вывода Клейна. В своей «Эрлангенской программе» он сводит математику к исследованию инвариантных преобразований и классифи­цирует математику в соответствии с этой иерархией. Гаусс, будучи великим геометром, полагал сущность и красоту математики в теории чисел, ко­торая никоим образом не является предметом инвариант Клейна. Может быть, теория чисел не живёт на севере? В его программе есть несколько слов о множествах, показывающих его некомпетентность. Он написал, что преобразование является непрерывным, если смежные бесконечно малые преобразуются вновь в смежные бесконечно малые.

Разве в духе северной математики использовать бесконечно малые, этот реликт восемнадцатого века? Я недолюбливаю бесконечно малые, у меня на это свои причины, а теперь и тем более, благодаря этому новому пророку! Бесконечно малые, стремящиеся к нулю, не являются математи­ческим объектом вроде числа или фигуры.

Одинок ли Феликс Клейн? Гельмгольц в своих беседах («Rede»)¹¹ за­явил, что сила государства зависит от развития науки. Наука поддерживает моральные ценности. Он классифицирует нации по их вкладу в челове­ческую культуру. С этим нельзя спорить, но мы видим, как реализуют эту мысль. Даже Дедекинд в предисловии к третьему изданию своего « 11 До­полнения» высказался в духе Гельмгольца, несмотря на то, что его кольца и тела далеки от этой известной темы.

Немцев ошеломляла гордость за пышный расцвет науки и культуры своей страны. Трудно поверить, что во времена молодости Гаусса только французы были математиками. Но с 1810 года все жители стали гражданами Пруссии. Не далее как тридцать лет назад двери гимназии открылись перед каждым молодым человеком. Говорят, что в немецкоязычных странах рас­положено около пятидесяти университетов. Мы чувствуем себя, как греки, или, скорее, как германцы времён распада Римской империи, как те герои «Песни о Нибелунгах», которая начинается так:

Полны чудес сказанья давно минувших дней
Про громкие деянья былых богатырей,
Про их пиры, забавы, несчастия и горе,
И распри их кровавые услышите вы вскоре.

Тот же дух, но в форме бетховенских квартетов, можно наблюдать на славных камерных университетских вечерах.

Что-то вскипает и приближается к нам. Все зачитываются книгами Гейне¹², который предостерегает нас, что за потрясающей музыкой Бет­ховена и нашей великой философией поднимается великая волна. Сила её гораздо больше той, которая ввергла просвещённых людей прошлого века в хаос революции. В народе распространены предрассудки. Они не про­пустят стен университетов. Известный физик Цёлнер использует спири­тические сеансы для поисков четвёртого измерения, идею которого он за­имствовал у Клейна.

Я позволю себе присоединиться к этому бессмысленному хору, введя рельефную букву алеф из иврита для обозначения классов равносильных друг другу множеств.

Съезд в Галле. Все берлинцы были против этого съезда, считая, что и без него они едины. Кронекер был вообще против собраний. Он сказал, что характер его математической деятельности таков, что он, как и прежде, хочет, чтоб его оставили в покое. В этом отношении я с ним согла­сен. Я тоже не люблю спектакли. Однако в круге математики есть много во­просов, которые должны решаться всем сообществом. Ещё в Гейдельберге я убедил большинство коллег собраться вместе для того, чтобы решать эти вопросы собственноручно. Галле был выбран для первого заседания Ассо­циации, мне поручили организацию. Мы ожидаем большое количество ма­тематиков. Несмотря на свои предыдущие вежливые письма, Кронекер не будет участвовать из-за болезни жены.

Но Клейн, Гильберт и Минковский из Геттингена будут присутство­вать. Миттаг-Леффлёр объявил о своём прибытии. Я спросил его, сколько спален мне нужно приготовить. Было много суеты, но я понял, что из меня получился неплохой организатор. Большую часть времени я проводил, от­вечая на письма. Кроме того, я приготовил научную программу съезда и проект будущего «Jahresbericht DMV» (годового отчёта немецкого мате­матического общества).

Идея нового Гёттингена возникла у Клейна и его коллеги Альтхофа, ди­ректора Министериума (муниципальное образование) в Берлине.

Целью Клейна было победно войти в Геттинген. Он хотел ввести там «математическое правление», переманив молодёжь в лице Гильберта и Минковского. Перед глазами встаёт «pontifex maximus mathematicus» (папский титул) Второго рейха. Даже Вейерштрасс побаивается и не при­едет в Галле. Не следует подчёркивать национальные особенности в науке, хотя я согласен с умеренными убеждениями Гельмгольца. Я считаю, что наш съезд будет важным шагом к объединению профессиональных матема­тиков нашей страны. Но после съезда я намерен связаться с математиками Франции и России для дальнейшего сотрудничества. Первым будет Васи­льев из Казани. Проведённые мной в Петербурге юные годы будут способ­ствовать тому, чтобы ему написать.

Шекспир и Бэкон. Окружённый повседневной суетой, я с удовольстви­ем вспоминаю прошедший в Галле съезд, и то, как хорошо мне удалось пре­одолеть все трудности. Теперь мне понятно, почему люди других профес­сий не испытывают такую усталость, даже если их работа была огромна. Они почти сразу могут увидеть результаты своей работы. Не так уж много нужно ждать для подтверждения ценности сделанного. Даже ошибки не огорчают их, потому что можно объяснить всё несовершенством мате­риала. В математике подмостки — это мир наших мыслей. Таким образом, только наши мысли виноваты в наших ошибках, но мои мысли — это я сам! Мы непрерывно видим себя в зеркале нашей деятельности. Какое облег­чение испытываешь, отстранившись от ежедневной работы, от призрака нашего внутреннего Минотавра. Мне приходилось видеть, как даже очень умные люди бежали на административные должности для того, чтобы на­ходиться в реальном круговороте событий.

Работа историка и литературоведа, даже исследователя, кажется мне довольно спокойной. Чтобы вырваться из моей эмоциональной математи­ки, я посвятил пять лет разгадке тайны Шекспира, тщательно исследуя ги­потезу — не мою, — суть которой состояла в авторстве Фрэнсиса Бэкона. Здесь я ни разу не встречался с вопросами, ответ на которые может быть «да» или «нет», ответ содержится в допущении «это зависит от…». Мной руководило какое-то высшее чувство, я самозабвенно работал в библио­теках, отдавая свой труд и силы, но это было благотворно для моего ума и души. Но я перестал завидовать спокойствию историков и литературове­дов, лишённых тех эмоций, которые даёт математика.

Лавина множеств. Теперь никто не протестует против множеств. Моя новая статья была опубликована в «Mathematische Annalen». Она отличает­ся от других статей объёмом рельефных еврейских алефов. Для некоторых именно алефы будут тревожным знаком…

Так как мощность множеств не ограничена, лестница моих трансфи­нитных чисел получила новый смысл. Она никогда не кончается! Беско­нечность моей лестницы символов абсолютна! Сегменты лестницы пред­ставляют множества одной и той же мощности. Но имеются ли сегменты, представляющие мощность континуума?

Лестница в целом свободно отражает всю математическую реальность. В обзоре книги Фреге я высказался против неопределённого понятия мощ­ности как общего обозначения множеств, эквивалентных данному, когда не указывают, как они образовались из данного множества. В те времена на роли таких объектов я рассматривал только натуральные числа, множества натуральных чисел и множество моих чисел второго класса.

Сейчас среди других внутренних отрезков моей лестницы чисел я рас­сматриваю бесконечно много претендентов, образующих восходящую трансфинитную последовательность множеств, различных по мощности. Я думаю, что для каждого хорошо определённого множества должна быть определена мощность в строгом смысле. Но в этом смысле я сомневаюсь прежде всего в отношении континуума, видя мои прежние мучительные воспоминания. Во всяком случае, я уверен, что совокупность всех моих чи­сел, так же как и множество всех множеств, не вполне определена, и они не могут быть представлены как множества. Таким образом, не всякую сово­купность можно пригласить танцевать.

Васильев. Наконец-то я нашёл время написать письмо. Я немного знаю о Васильеве¹³. Моё знание русских обычаев облегчает написание пер­вых слов. Я написал о будущем Конгрессе. Но я не мог отказать себе в удо­вольствии вспомнить детские годы в Петербурге. Я уехал из Петербурга, когда мне было 11 лет. Я помню облака над широкой мрачной Невой. Я со­гласен со словами «Север пленяет». Отцовские дела были закончены, он решил провести остаток жизни в Германии. Фактически в Петербурге он был иностранцем, прибывшим из Копенгагена, где мой дед занимал вид­ное место в еврейской общине. Я помню Петербург как притягательный многокультурный город. Только по приезде в Германию я узнал о тамошней математической жизни. Васильева интересовали международные связи и организация Конгресса.

Эрмит. Мой интерес к Бэкону сблизил меня с Эрмитом. Как это часто бывает среди математиков, его разнообразные интересы выходили далеко за пределы математики. Наши взгляды во многих областях совпадали. По­чему математики чаще других людей ищут новые результаты в постоянной погоне за признанием? Я знаю это по моему собственному опыту. Эрмит, чьи усилия были действительно велики, мог отвергать то зеркало, в которое я постоянно смотрелся. Его авторитет обеспечивает ему большое влияние. Он всегда невозмутим, и мне передаётся его хладнокровие. В нашей пере­писке множества не упоминаются. Я знаю, что он против них. Темы нашей переписки лежат за пределами математики.

По Европе бродят суеверия и призраки обречённости. Во Франции распространяются масонство и оккультизм. В Германии непомерный культ нации и государства. Хотя это, кажется, противоречивые тенденции. Люди отвергли христианскую традицию, которая всегда сдерживала мысли и предотвращала конфликты.

Недавно меня попросили рекомендовать кого-либо на должность во Фрайбург. Я назвал известного мне молодого студента-математика Гуссер­ля. Я немного знал его, он был лучшим из семерых кандидатов. Но Гуссерля отклонили. Несомненно, тому причиной его еврейское происхождение. Я изложил своё мнение, упомянув о его глубокой приверженности лю­теранской традиции. Заметно, что Гуссерль не более чем деист, пантеист, фактически он ещё не определился. Я защищал его с помощью обтекае­мых аргументов, не усмотрев в его деизме никакой опасности, хотя все эти «измы» где-то потом собирались воедино.

Предубеждённость, которая сначала замечалась в народе, теперь пе­редалась науке, где приобрела опасную окраску. Не свойственные науке взгляды проникли сквозь стены университетов, где стали основой для ре­лигиозного и национального соперничества. Седовласый Гельмгольц ут­верждал, что наука улучшает общество. При этом мы видели, что наука слу­жит не нуждам благосостояния, а удовлетворению политических амбиций. Неужели будущие математические конгрессы будут полями сражений?

В самом начале христианство противостояло иудаизму, но можно ска­зать, что это был высший уровень творения. Не всякому я могу довериться, но вот, например, Эрмита я мог спросить, кто был на самом деле Иосиф Аримафейский. Мы либеральные люди, но мы тесно связаны с религиоз­ной традицией, которая даёт нам некоторое право на ересь. Но в наше вре­мя религия — это знак идентификации. Не то чтобы это было очень важно, но мы задаём вопрос: «Где вас крестили после рождения?». Мой отец, воз­можно, не понял бы меня, его письмо, которое я храню до сих пор, прони­зано мыслями о Боге. Это письмо было написано мне, когда я начал учиться в Цюрихе, и до сих пор оно является основой моих взглядов. Но в письмах к Эрмиту я часто предстаю свободомыслящим, даже употребляю фразы а ля Ренан. Я люблю пошутить, но немногие знают меня с этой стороны.

Embarrasderichesse. (Затруднение от избытка). Теперь ничто не мешает мне видеть мою шкалу чисел ничем не ограниченной. Гильберт сказал, что это повлечёт противоречия, так как сама по себе шкала вполне упорядочена, и, следовательно, она должна быть одним из основных сег­ментов. Однако это не более чем софистические разногласия, которые могут быть удалены, если мы найдём способ отделять всю шкалу от её сег­ментов. У меня было похожее противоречие со II классом моих чисел, но я непосредственно могу показать, что с учётом их несчётности они не могут быть исходными сегментами для себя самих.

Я ввёл мои чистые множества итеративно. Начал с множеств, уже из­вестных в математике, получая новые на основе множеств, введённых ра­нее. Я убеждён, что правомерно рассматривать семейство подмножеств уже известного множества. Я показал Гильберту список операций, с по­мощью которых можно получать множества из уже имеющихся. Но я опа­саюсь, что он принял его за список аксиом.

Среди правил образования новых множеств я не вижу такого, которое позволяло бы образовывать совокупность моих чисел как множество, как это было в случае чисел второго класса. Но принять всю шкалу как мно­жество означало бы получить противоречие. И я воздержался от этого. В этом отношении я свободен.

Самая запутанная ситуация с теми множествами, которые я называю готовыми (ready). В математике они известны, но они могут быть чуждыми для моей итеративной теории множеств. Есть разница между абстракт­ным множеством и множеством, которое воспринимается в математике как данность. Я воспринимаю его как множество чистых единиц, как услов­ность белого билета. Условность белого билета более либеральна. К ним я и отношу континуум. К континууму не применимы связи «принадлежит к…». Такая же трудность состоит в описании его подмножеств. Но без этих инородных объектов моя теория лишится математического содержания. Для итеративно определяемых множеств важна только их структура, и при описании достаточно только отношение членства.

В Гарцбурге к нашей беседе с Гильбертом ненадолго присоединился Дедекинд. Несмотря на то, что ему была интересна наша дискуссия, он бы­стро покинул нас, потому что уходил последний дилижанс на Брауншвейг.

Почти двадцать лет назад я сформулировал теорему сравнения мощно­сти множеств (Zwischenmengensatz). Сейчас её проверил молодой Феликс Бернштейн. Он рассмотрел сжатие сегмента на сегмент, из которого уда­лена концевая точка. Мыс Дедекиндом упустили из виду, что эта ситуация легко обобщается. Наиболее интересно, что доказательство проводится для тех множеств, которые относятся к условным белым билетам.

Большая часть проблем теории множеств разошлась по другим мате­матикам. Я не возражаю, чтобы теория множеств стала общим достоянием математиков. Я поставил и сформулировал проблемы. Сейчас я вспоминаю пророчество из моей диссертации: математика — это искусство ставить во­просы (the art of proponendi questionem…). Я помню свой страх перед беотийцами, когда я был занят сложными доказательствами второстепенных те­орем. Теперь моя теория стала зрелой, и я свободен от страха за её будущее.

Письмо из клиники для душевнобольных. Мне стали свойственны пло­хие мысли. Именно на это указывал Миттаг-Леффлёр в одном из писем. Но мы всегда можем прочитать в Евангелии, что всё зло в нас самих, и что­бы избежать этого, нужно идти к людям. Я чувствую, как мне не хватает Кронекера, истинно чистосердечного и открытого, с которым можно по­говорить о том, что меня беспокоит. В наших беседах с Дедекиндом я чув­ствовал себя скованно, он подавлял меня своей мудростью. Достигнув пя­тидесяти, я заметил, что становлюсь старше Дедекинда, который всё время общается с молодёжью. Я никогда не выдвигал докторов. Общение с моло­дым Гильбертом было скорее поверхностным и прохладным. В математике он чувствовал себя независимым. Мне кажется, он всё подчиняет доктрине аксиоматизации. Сейчас я пишу Гильберту, подшучивая над местом свое­го пребывания. Это университетская клиника нервных болезней. Биогра­фы согласятся, что я сохранял невозмутимость даже в трудных ситуациях. Я верю, что благодаря моей теории и не в меньшей степени благодаря моим оппонентам они будут испытывать ко мне признательность.

Был ли среди моих оппонентов Дедекинд? Его философия, опубли­кованная позже в «Что такое числа и для чего они служат?», объясняет происхождение натуральных чисел, это было мне известно ещё до нашей встречи в Интерлакене. Жаль, что наши беседы ограничивались арифмети­кой. В то время у меня был скромный философский опыт, недостаточный для понимания его глубоких идей. Теперь я уже в состоянии поднимать се­рьёзные вопросы, касающиеся философии множеств и чисел. Но когда мы этим летом случайно встретились в Гарцбурге, наш разговор прекратился после нескольких слов. Спустя несколько дней я написал ему письмо с во­просом о множествах, которые назвал вполне определёнными. Его ответ был очень вежлив. Он написал, что этот серьёзный вопрос весьма далёк от его нынешних интересов, и при его обсуждении сам он оказывается в роли дилетанта. Это нежелание обсуждать со мной вопрос или уход от ответа? Я спросил, принимает ли он систему натуральных чисел как множество? Думаю, что это утверждение сходно с принятием трансфинитного. Пом­ню последнее из писем, посланное ему в восьмидесятые. Я тогда впервые сообщил ему о трансфинитных числах, а он принял это без всякого энтузи­азма. Его математика ограничена понятиями, которые тщательно опреде­лены и детально проработаны. Он критикой встретил мою теорию чистых множеств, но я слышал, что мои числовые классы приняты им как возмож­ные обозначения мощности.

Я вновь обращаюсь к нашей переписке семидесятых. У меня была ил­люзия взаимопонимания. Но в письмах он выглядел как школьный учитель, за которым остаётся последнее слово. Для него важна была лишь правиль­ность доказательства. Идеями мы не обменивались. Полагаю, в этом я не был исключением. Общался ли он с Дирихле, когда писал «Supplement» (Дополнение) к его идеям. Фактически, это были его собственные идеи, которые он сам прорабатывал годами. Возможности совокупности нату­ральных чисел перестают удивлять, если отвлечься от их глубокого смысла, заключающегося в мысленном обращении к самим себе, определении через самих себя. В аксиоматизации Пеано они делаются тривиальными. Пола­гаю, что идея Дедекинда о потоке мышления никогда не обсуждалась среди математиков. Для поддержки своих идей он обратился к Больцано. Погру­жённый в мир собственных мыслей, он не нуждался в близком общении с другими математиками. Теперь мне легче понять его «Treppenverstand».

Сейчас он обменивается вежливыми письмами с Феликсом Бернштей­ном. Не удивлюсь, если через несколько лет у него на книжной полке образу­ются записи с кратким очерком основной идеи доказательства Бернштейна.

В общении обходительность его казалась лишённой сопереживания. Он мягкий человек и избегает неприятных слов. Поэтому он пользуется ре­путацией дружелюбного человека. Иными словами, он не склонен к враж­дебности. Плюсы и минусы в его выражениях находятся в относительном равновесии.

Когда-то я был неприятно поражён нашим резким разрывом. Года­ми отношения были дружелюбными, а затем внезапно и без объяснений были им прекращены. Чтобы избежать погружения в депрессию, я выдви­нул в качестве причины внутренних страхов неприязнь Кронекера. В то же время я придал Дедекинду отталкивающие черты бездушного старца. Та­кой недостаток часто встречается в характере математиков.

Гипотеза континуума могла бы быть отвергнута, если бы мы знали, что континуум не может быть представлен как алеф. На Конгрессе в Гейдель­берге в 1904 году Кёниг предложил изящное доказательство этого. Кантор присутствовал на заседании и был глубоко поражён выступлением Кёнига. Но на следующий день Цермело представил доказательство того, что каж­дое множество может быть вполне упорядочено. Эти два результата проти­воречили друг другу.

Нет сомнений в правильности доказательств Цермело. Однако цен­ность его обсуждалась. В доказательстве использовался приём, называемый ныне принципом выбора. Цермело доказал, что вполне упорядоченное множество определено с помощью свободного выбора точек из подмно­жества данного множества. Значение этого принципа может оспаривать­ся, так как возможность такого отбора лишь постулируется, но его не всегда возможно осуществить конструктивно.

Тень Дедекинда долго всё омрачала. Судя по замечанию Цермело, его знаменитое доказательство было основано на старой идее Дедекинда из книги «Что такое числа и для чего они служат?», позволившей ему пред­ставить его конечные множества на шкале натуральных чисел.

Как бы то ни было, благодаря открытию Цермело идеи Кантора пред­стали теперь в полном освещении. Его теория родилась заново. Его шкала трансфинитных чисел, которую раньше рассматривали как игру символов, стала исполнять роль математического абсолюта.

Встреча в Интерлакене вынудила Кантора принять драматическое ре­шение по выбору своего собственного пути в математике. Дорого запла­тил он за отказ от обычного жизненного пути профессора математики. Он был один на один со своими проблемами, без ободрения математическо­го сообщества. Отношения с Дедекиндом были не просто холодными, за долгие годы он проявился как деспотический Бог Отец или, пожалуй, как собственный отец Кантора, отговаривавший его от математики как объ­екта исследования.

Однако в свои последние годы Кантор не поминал прошлое. Он был окружён почётом. Его теория стала популярной в Англии. Он никогда не восхищался математикой англичан, но саму Англию ценил как одну из вершин цивилизованного мира. Членство в Лондонском математическом обществе и почётный докторат Университета Св. Андрея позволили ему посетить остров своей мечты. Его старые проблемы по поводу располо­жения мощностей множеств на шкале трансфинитных чисел стали извест­ны в Англии благодаря Харди. Дискуссии вокруг антиномий Рассела были тягостны для Кантора. Он считал их не более чем следствием логических недоразумений.

Были почётные звания из Христиании и из Харькова. Но не из Берли­на! До Кантора дошли поразительные известия о выступлении Пуанкаре на

Конгрессе в Риме в 1908 году с яростными нападками на теорию множеств. Ещё раньше он слышал о Пуанкаре как о французской реплике Клейна. Сейчас он признаёт, что можно было зайти ещё дальше в грубости выра­жений, соревнуясь с немецким «pontifex maximus». В письме Эрмиту он писал, что французский Клейн присвоил себе право принимать решения от имени всех математиков, хотя сам он прост и примитивен и высказы­вается, не зная темы. Самое удивительное было то, что Пуанкаре снискал овации участников конгресса за своё выступление, в котором содержались ядовитые насмешки над немецкой теорией и заодно над немецким словом «menge» (множество). Но теперь Берлин предложил ему стать членом Академии.

В 1908 году Эрнст Цермело под давлением Гильберта переформулиро­вал теорию множеств в аксиоматическую систему. Эта идея представлялась Кантору чуждой. Гильберт, Бернштейн, Шварц и многие другие приехали в Галле по случаю семидесятилетнего юбилея Кантора. Дедекинд одиноко жил в Брауншвейге. Полным ходом шла мировая война.

Добавление после того, как текст был закончен. Автора всегда удив­ляло, что в большинстве книг, посвящённых развитию теории множеств, был большой пробел. Имя этому пробелу — Рихард Дедекинд. Среди математиков-основателей теории множеств только Эрнст Цермело при­давал Дедекинду решающую роль в решении важных вопросов теории, а также в создании идей непреходящей важности. После долгих поисков в литературе автор наконец-то нашёл две работы. Одна из них — это очерк Маккарти («Mysteries of Richard Dedekind», David McCarty), который дал широкий обзор идей Дедекинда и их влияния на современную математи­ку. Другой исторический очерк Феррейроса (Jose Ferreiros «On the Rela­tion between Georg Cantor and Richard Dedekind», Historia, Mathematica 20 (1993), p. 343-363), где роль Дедекинда была представлена в соответствии с фактами и внутренней правдой математической жизни. Но в истории, из­ложенной здесь, ничего не следует менять, даже ради улучшения. Услов­ность этой истории даёт автору некую долю свободы в лавировании между фактами и эмоциональной окраской. Но позвольте в конце привести сло­ва, выбранные Хосе Феррейросом в качестве эпиграфа, которые красной нитью проходят через весь текст: «Наш разрыв был для меня настолько болезненным, что все эти годы я посвятил тому, чтобы представить мои внутренние математические убеждения на ваш суд», — из письма Кантора к Дедекинду 1882 года.

* * *

Скажем теперь несколько слов о Канторе. Кантор провёл лето 1900 года в клинике нервных болезней. Он не принимал участия в Париж­ском Конгрессе. Знал ли он, что Гильберт включил в свой список проблем теорию множеств? Хотя Кантор питал к Гильберту некоторую привязан­ность, он не смог удержать горького замечания, что «göttingener mathematishes Regiment» (гёттингенская математическая верхушка) заявила о своём стремлении лидировать в математическом сообществе. Порадо­вало ли Кантора, что гипотеза континуума была без согласования с ним включена в список мировых проблем? Видел ли он себя ненужным уже че­ловеком среди своих собственных проблем?

К Кантору приходили известия, смягчённые оградой клиники нервных болезней. Не все они достигли Кантора. Молодой Эрно Юргенс опубли­ковал работу, в которой заявил, что доказательство Кантора о том, что ев­клидовы пространства, отличающиеся размерностью, не могут быть во вза­имно-однозначном непрерывном соответствии, необоснованно (ist nicht stichhaltig). Юргенс вспомнил старое доказательство Люрота, которого Кантор презирал, для размерностей 2 и 3, и представил ещё и своё соб­ственное доказательство. Кантор никогда не упоминал своё злополучное доказательство, исключив его из памяти.

Перевод с польского Г. И. Синкевич

Ежи Медушевский. Георг Кантор о Дедекинде, Кронекере и о самом себе. // «РУССКИЙ МIРЪ. Пространство и время русской культуры» № 8, страницы 271-299

Скачать текст

 

 

Примечания автора

 

1. Часто встречается мнение, что Кантор случайно пришёл к идее множеств, исследуя тригонометрические ряды. Но мы должны иметь в виду известное биографам школьное восхищение Кантора молекулярной теорией материи.
2. Возможность деления бесконечных множеств на две части, т. е. представления их мощности m в форме m+m, кажется очевидным, но доказательство, данное Г. Гессенбергом в 1916 году и основанное на принципе выбора, непросто. См.: W. Sierpiński, Cardinal and ordinal numbers, Warszawa 1958, p. 416.
3. Можно предположить, что идея Дедекинда из «Was sind was sollen die Zahlen?» была известна Кантору, будучи неявно выраженной в «Supplement 11», 1863. (Дедекинд, 11 Дополнение).
4. Моисей Мендельсон (1720-1768) — философ, автор важной для математики работы «Uber die Evidence in metaphysischen Wissenschaften», 1753.
5. Дата, указанная Дедекиндом, может быть установлена по его предисловию к « Stetigkeit und irrationale Zahlen», 1872.
6. Доказательство Кантора о размерности было непросто ошибочным, а заведомо неверным, как двадцать лет спустя заявил Эрно Юргенс. Но одновременно с доказательством Кантора верное доказательство невозможности взаимно-однозначного соответствия между пространством и плоскостью дал Якоб Люрот. Подробности в статье Джонсона (Dale М. Johnson). Полное решение проблемы было дано Брауэром (L. E. J. Brouwer, 1911). Ключ доказательства заключался в теореме об инвариантности области, которую Дедекинд обсуждал с Иоганном Томе (Johannes Thomae). Подробности в статье Джонсона (Dale М. Johnson, 1979).
7. Об отношениях между Гёте и Гауссом автору известно из статьи К. R. Birmann «Göthe und Gauss».
8. Известное Канторовское «троичное множество» было описано в «Метопе Nr 5» в маленьком примечании.
9. «Memoire Nr 5» из «Über unendliche lineare Punktmannigfaltigkeiten» (1883) следует рассматривать как наиболее важную работу Кантора о множествах. Однако это не помешало Жану Кавай назвать некоторые отрывки из этой работы многословными.
10. Известное письмо «Versohnungbrief» содержится в сборнике «Georg Cantor. Briefe», Springer.
11. Hermann von Helmholtz (1821-1894) — «Über die tatsächliche Grundlagen der Geometrie».
12. См..: Heine H. Zur Geschichte der Religion und der Philosophie in Deutschland (1834).
13. Александр Васильев (1853-1929) — профессор математики в Казани.